若设随机试验E的样本空间为Ω，B₁，B₂，…，B_n是一个完备事件组，且P(B_i)>0(i=1，2，…n)，则对E的任一事件A，都有：

P(A)=P(B_i)P(A|B_i)+P(B₂)P(A|B₂)+...+P(B_n)P(A|B_n)

上式称为全概率公式。

利用全概率公式，我们可以通过综合分析一个事件发生的不同原因、情况或途径及其可能性来求得该事件发生的概率。假若我们要考虑与之完全相反的问题，例如观寨到一个事件已经发生，现在需要了解该事件发生是由其各种原因、情况或途径等中的哪一个引起的，这时我们就要采用下列公式来解决：

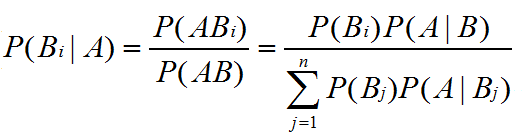
上式称为逆概率公式，或称为贝叶斯公式。

在全概率公式和贝叶斯公式中的B₁，B₂，…，B_n是导致事件A发生的各种原因、情况或途径及其可能性。P(B_i)(i=1,2，…，n)是各种原因发生的概率，称为先验概率，一般由实际经验给出。贝叶斯公式中的P(B_i|A)称为后验概率，它反映了事件A发生后各种原因B_i(i=l,2，…,n) 成的可能性的大小。