快速查题-中级统计师试题
中级统计师
筛选结果
共找出111题
- 不限题型
- 不定项选择题
- 判断题
- 单选题
- 多选题
- 简述题
回归分析的目的有( )。
- A
确定两个变量之间的变动关系
- B
用因变量推算自变量
- C
用自变量推算因变量
- D
两个变量相互推算
- E
确定两个变量间的相关程度
相关关系按其变动方向的不同可分为( )。
- A
完全相关
- B
负相关
- C
非线性相关
- D
不完全相关
- E
正相关
估计标准误差的作用是表明( )。
- A
回归方程的代表性
- B
样本的变异程度
- C
估计值与实际值的平均误差
- D
样本指标的代表性
- E
总体的变异程度
回归系数和相关系数的符号是一致的，其符号均可用来判断现象( )。
- A
线性相关还是非线性相关
- B
正相关还是负相关
- C
完全相关还是不完全相关
- D
单相关还是复相关
根据相关系数r的特点，下列对r取值的意义表述正确的是（ ）。
- A
r 值若趋近于+1，表示 x与y变量之间线性相关程度密切，趋近于-1表示不密切
- B
r=0表示两个变量之间不存在任何相关关系
- C
在大多数情况下， 0≤丨r丨<1表示 x与y变量之间存在一定的线性关系
- D
丨r丨永远不会等于1
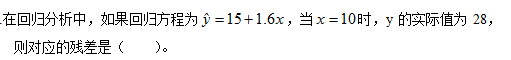
- A
-15
- B
-3
- C
3
- D
16
在一元线性回归分析中，若相关系数为r，回归方程拟合程度最好的是（ ）。
- A
r=0.75
- B
r=-0.97
- C
R2=0.75
- D
R2=0.90
对居民收入Y与消费支出X的几组不同样本数据拟合直线回归方程中可能正确的是（）。
- A
Y=-40+9X
- B
Y=120-10X
- C
Y=130-3X
- D
Y=-16-8X
回归系数的含义为（）。
- A
洗洁精含量增加一个单位，泡沫高度平均增加0.755 毫米
- B
洗洁精含量增加一个单位，泡沫高度平均增加9.50 毫米
- C
泡沫高度增加一个单位，洗洁精含量平均增加4.22毫米
- D
泡沫高度增加一个单位，洗洁精含量平均增加2.679毫米
下列现象的相关密切程度最高的是( )。
- A
某商店的职工人数与商品销售额之间的相关系数是0.87
- B
流通费用水平与利润率之间的相关关系为-0.92
- C
商品销售额与利润率之间的相关系数为0.51
- D
商品销售额与流通费用水平的相关系数为-0.81
