快速查题-监理工程师试题
监理工程师
筛选结果
共找出220题
- 不限题型
- 单选题
- 多选题
- 简述题
工程网络计划的优化目标有（ ）
- A
降低资源强度
- B
使计算工期满足要求工期
- C
寻求工程总成本最低时的工期安排
- D
工期不娈条件下资源需用量均衡
- E
资源限制条件下工期最短
关于工程费用与工期在一般情况下的关系，说法正确的有( )。
- A
工期延长.工程总费用一定增加
- B
工期缩短，工程总费用一定增加
- C
工期缩短.直接费用随着增加
- D
工期缩短，工程间接费用随着增加
- E
工期缩短，间接费用一般随着减少
某分部工程中各项工作间逻辑关系见表3-9，相应的双代号网络计划如图3—63所示，图中错误有( )。
- A
多个终点节点
- B
多个起点节点
- C
工作代号重复
- D
不符合给定逻辑关系
- E
节点编号有误
某工程双代号网络计划如下图所示，图中已标明每项工作的最早开始时间和最迟开始时间，该计划表明（ ）。
- A
工作1-3的自由时差为2
- B
工作2-5为关键工作
- C
工作2-4的自由时差为1
- D
工作3-6的总时差为零
- E
工作4-7为关键工作
在网络计划的工期优化过程中，为了有效地缩短工期，应选择( )的关键工作作为压缩对象。
- A
持续时间最长
- B
缩短时间对质量影响不大
- C
直接费用最小
- D
缩短持续时间所需增加的费用最少
- E
有充足的备用资源
在单代号网络计划中，如果工作只有项紧后工作j。则工作i的总时差等于( )。
- A
工作1的最迟完成时间与工作i的最早完成时间之差
- B
工作j的最早开始时间与工作i的最早完成时间之差
- C
工作1与工作j的时间间隔加上工作J的总时差
- D
工作j的最迟开始时间与工作i的最早开始时间之差
- E
工作j的最早开始时间与工作i的最迟完成时间之差
某分部工程双代号时标网络计划如图3-66所示，该计划所提供的信息有( )。
- A
工作B的总时差为3天
- B
工作C的总时差为2天
- C
工作D为关键工作
- D
工作E的总时差为3天
- E
工作G的自由时差为3天
某双代号网络图如图3-1所示，互为平行工作的有( )。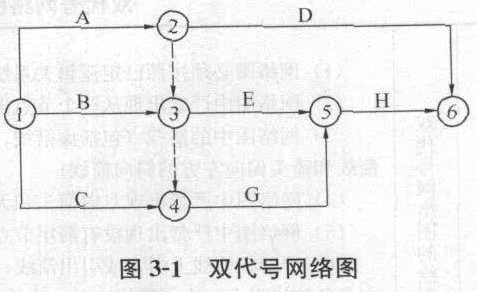
- A
工作A和工作B
- B
工作A和工作E
- C
工作A和工作G
- D
工作B和工作G
- E
工作B和工作C
某工程项目双代号时标网络图如图3-59所示.则( )。
- A
工作的最早开始时间为10
- B
工作D的总时差为3
- C
工作C的自总时差为2
- D
工作C的最迟开始时间为2
- E
工作D的最迟完成时间为1
某分部工程双代号网络计划如图3—61所示(时间单位：天)，图中已标出每个节点的最早时间和最迟时间，该计划表明( )。
- A
所有节点均为关键节点
- B
所有工作均为关键工作
- C
计算工期为15天且关键线路有两条
- D
工作1一3与工作1—4的总时差相等
- E
工作2—7的总时差和自由时差相等
© 2024-2024 koolearn.com 版权所有 全国客服专线：400-676-2300
京ICP备2024050960号-2
京公网安备11010802044296号
ICP许可证编号:京B2-20241156
信息网络传播视听许可证：0110531
新东方教育科技集团旗下成员公司